Olopoiema nelle strutture naturali
1) Cefalopodi fossili
§ 9. A un'esposizione puramente geometrico-matematica delle
caratteristiche di Olopoiema, con i relativi riflessi di tipo
naturalistico, preferiamo - per ragioni di evidenza - seguire il
procedimento inverso: partire, cioè, dalla natura, fornendo le istruzioni al
programma atte a descriverla e insieme utili a illustrare le proprietà del
programma medesimo.
Prendiamo in esame - per cominciare - un Orthoceras, mollusco della
classe dei Cefalopodi, vissuto tra il siluriano del paleozoico e il triassico
del mesozoico.
E' un Nautiloide a conchiglia ortocona, cioè a forma di
cono diritto, effetto di una propagazione concentrica in traslazione assiale. Presenta
l'aspetto della concamerazione a rapporto costante, con setti concavi
divisori costruiti dal fenomeno della pulsazione (sez.III, "La
gravitazione ondulatoria", cap.IV b), parte prima). Il senso
centripeto della conchiglia (verso il vertice del cono) incontra le concavità
dei setti, per il motivo già rilevato nei Nautiloidi in generale al cap.VI di
quella sezione (La strutturazione gravitazionale, § 15).
Ricorriamo, quindi, ad Olopoiema nel sottoprogramma
"Propagazione", con i dati iscritti nella finestra degli input (Inserimento
Valori), come si mostra nella seguente fig.1, e confrontiamone il risultato
grafico con gli organismi fossili reali di fig.2.


Fig.1

Fig.2
§ 10. Il rapporto a'/a = 0,999, di quasi equintensità
tra le sorgenti componenti (a'/a = 1 darebbe errore al computer), è
posto con un valore superiore a quello limite tra una propagazione composta
eccentrica - a spirale logaritmica - e una concentrica -a spirale archimedea -
(per cui v. sez.III, cap.IV a), La "composizione ondulatoria",
§ 22): tale da corrispondere a un angolo costruttivo (ivi, § 5) prossimo a
zero, come si legge nell'ultimo rettangolo degli input, facendo clic nel primo.
TE = 0,2 è il valore di differenza tra radici quadrate
successive di numeri interi, supposto come critico perché si verifichi una
pulsazione tra onde concentriche consecutive (cap.IV b), parte prima,
§§ 10-11).
N è il denominatore di frazione (ivi, §§ 4-5
per la propagazione eccentrica e §§ 10-11 per la concentrica) che riduce
l'incremento di lunghezza d'onda dopo ogni pulsazione e, quindi, accresce
proporzionalmente la fittezza delle pulsazioni: ovvero, nel caso delle
conchiglie, il numero dei setti. Nel grafico risultante da Olopoiema (fig.1) la
pulsazione marca l'intera onda di strutturazione (sez.III, cap.VI), mentre in
natura la materia si addensa gravitazionalmente, in ogni onda pulsata, nell'emisfero che presenta la
concavità - come detto al paragrafo precedente - alla direzione centripeta della conchiglia (procedendo verso il
vertice del cono, all'incrocio grafico dei due assi cartesiani). L'aase
orizzontale, interno alle linee di forza, segna il vuoto del tubo
sifonale.
NT attribuisce un numero di unità di lunghezza per
unità di tempo (ossia una velocità lungo l'asse di traslazione) alla crescita
dell'animale, che abita l'ultima camera della conchiglia. Nel grafico disegnato da Olopoiema in
fig.1
appaiono, tra le onde pulsate, le più sottili
onde di interincidenza (si veda in sez.III il cap.IV b), parte seconda),
in numero crescente tra setti successivi: la distanza tra essi, infatti, varia
secondo un rapporto costante, come si è detto.
Come sempre, raccomandiamo ai lettori di ripetere personalmente
l'operazione grafica, usando il programma offerto loro in sez.III, per la
straordinaria evidenza insita nello svolgimento temporale del processo che abbiamo
descritto.
§ 11. La potenza di Olopoiema diventerà sempre più
evidente a misura che proseguiremo nell'analisi della morfogenesi naturale.
Continuiamo intanto l'esame dei Nautiloidi fossili, leggendone prima la
descrizione che se ne fa nell'Enciclopedia Monografica di Scienze Naturale della
Mondadori:
I Nautiloidi, apparsi improvvisamente nel Cambriano
superiore, sono i cefalopodi più antichi. Essi sono particolarmente
interessanti per lo studio di tutta questa vasta classe, sia perché contano
ancora un rappresentante vivente, sia perché da questi sono derivati, nel corso
dell'evoluzione, sia gli Ammonoidi sia i più moderni Dibranchiati. I Nautiloidi
sono caratterizzati da una conchiglia esterna che assume forma assai diversa:
ortocona, se a forma di cono diritto, cirtocona, se leggermente ricurva,
girocona, quando avvolta pianispiralmente senza che i diversi giri si tocchino,
ofiocona, se i giri vengono a contatto ricoprendosi parzialmente o totalmente. A
questo riguardo, è interessante notare che durante il processo evolutivo si
ebbe una tendenza all'avvolgimento del guscio, che passò così da forme diritte
a forme avvolte a spirale con giri sempre più serrati fino a giungere alle
conchiglie del Nautilus, estremamente involute.
In fig.3 si riportano le forme ora descritte delle varie
conchiglie e nella successiva fig.4 la rappresentazione ricostruita di alcuni
degli animali primitivi.
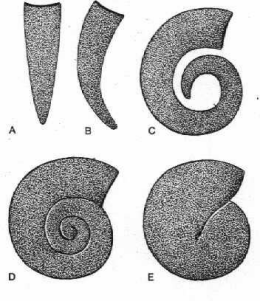
Fig.3

Fig.4
Operiamo ora col sottoprogramma "Strutture Raggiate"
di Olopoiema. Per passare dalla conchiglia ortocona di figg.1 e 2 a quelle
ricurve occorrono due principali cambiamenti. Il primo riguarda il rapporto a'/a,
che non sarà più di equintensità tra le sorgenti componenti (a'/a =
1), il cui risultato è una propagazione concentrica con traslazione
assiale, ma di disequintensità (a'/a < 1), col risultato di
una propagazione eccentrica a traslazione spirale. Per ridurre le strutture
raggiate a forme aradiali basterà porre come angolo divisore ED nella
finestra degli input il valore 0 o 360. Il secondo cambiamento
riguarda appunto la traslazione di campo, che da assiale diventa spirale. Solo
formale è la sostituzione del rapporto a'/a col corrispondente angolo
costruttivo della spirale (input A nella finestra: v. §§ 5 e 22 del
cap.IV a) nella sez.III; la conversione compare nell'ultimo rettangolo,
cliccando nei primi due solo ai fini del calcolo reciproco, come si capirà
provando). Si tenga anche presente che in questo sottoprogramma l'intervallo
angolare T tra i diametri delle onde è costante: ciò vuol dire
che il risultato grafico fornisce l'esito strutturante della pulsazione (setti
equiangolari), tralasciando quello dell'interincidenza (equidistanza lineare
sulla spirale), come invece sappiamo potersi rappresentare col sottoprogramma
"Propagazione".
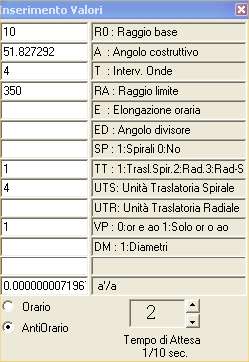
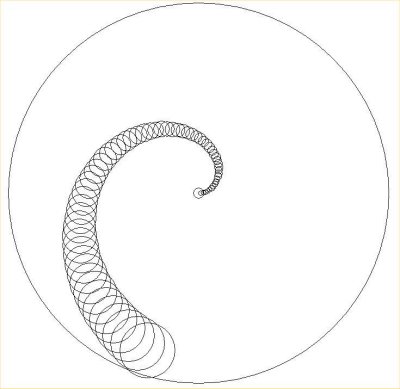
Fig.5
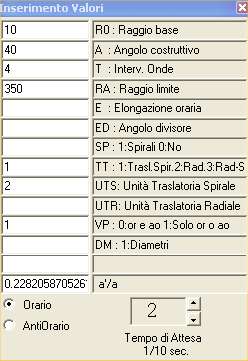
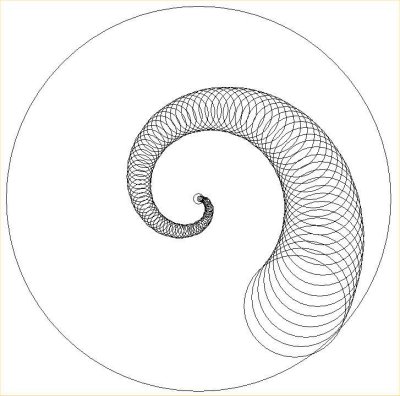
Fig.6


Fig.7
L'avvolgimento sempre più stretto della conchiglia attraverso
le figg.5, 6 e 7 - a forma rispettivamente cirtocona, girocona e ofiocona -
dipende dal crescere di a'/a (o dal decrescere di A) e dal
diminuire dell'unità traslatoria spirale. Nella fig.8 diamo una situazione di
transizione con separazione dei giri al centro e la loro tendenza a toccarsi e
poi a ricoprirsi verso la periferia, come abbiamo letto nella descrizione
dell'Enciclopedia Mondadori. Evolutivamente ciò corrisponde a una fase
intermedia tra la morfologia dei Nautiloidi e quella degli Ammonoidi, che
presentiamo conseguentemente nella fig.9.
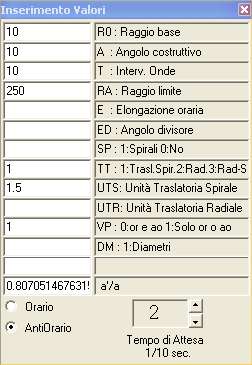

Fig.8

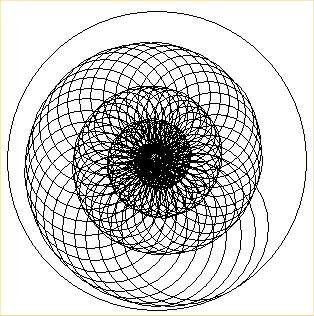
Fig.9














